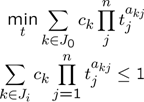
The following example requires MOSEK or GPPOSY, or any nonlinear solver such as FMINCON, SNOPT or IPOPT. The solvers GPPOSY is a dedicated geometric programming solvers but slightly outdated. With MOSEK, YALMIP automatically rewrites the problem to an [exponential cone program]((tutorial/exponentialcone). With a general nonlinear solver, it is possible tell YLMIP to rewrite the geometri program to its convex form.
A general signomial problem has the following form.
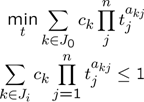
Geometric programming solvers are capable of solving a sub-class where \(c\geq 0\) and \(t\geq 0\), so called posynomial geometric programming. The following example is taken from the MOSEK manual. Note that there has to be explicit positivity constraint on all involved variables in the model.
Assuming MOSEK or GPPOSY is available, we can solve the following model.
sdpvar t1 t2 t3
obj = (40*t1^-1*t2^-0.5*t3^-1)+(20*t1*t3)+(40*t1*t2*t3);
C = [(1/3)*t1^-2*t2^-2+(4/3)*t2^0.5*t3^-1 <= 1, [t1 t2 t3]>=0];
optimize(C,obj);
If the geometric program violates the posynomial assumption, an error will be issued.
optimize(C + [t1-t2 <= 1],obj)
Warning: Solver not applicable
ans =
yalmiptime: 0.0600
solvertime: 0
info: 'Solver not applicable'
problem: -4
YALMIP will automatically convert some simple violations of the posynomial assumptions, such as lower bounds on monomial terms and maximization of negative monomials. The following small program maximizes the volume of a box, under constraints on the floor and wall area, and constraints on the relation between the height, width and depth (example from [Boyd et al. 2007]).
sdpvar h w d
Awall = 1;
Afloor = 1;
C = [0.5 <= h/w <= 2, 0.5 <= d/w <= 2, h>=0, w>=0];
C = [C, 2*(h*w+h*d) <= Awall, w*d <= Afloor];
optimize(C,-(h*w*d))
Some geometric programs, although not given in standard form, can still be solved using a standard geometric programming solver after some some additional variables and constraints have been introduced. YALMIP has built-in support for some of these conversion.
To begin with, nonlinear operators can be used also in geometric programs, as in any other optimization problems (as long as YALMIP can prove convexity and find a suitable graph representation)
sdpvar t1 t2 t3
obj = (40*t1^-1*t2^-0.5*t3^-1)+(20*t1*t3)+(40*t1*t2*t3);
C = [max((1/3)*t1^-2*t2^-2+(4/3)*t2^0.5*t3^-1,0.25*t1*t2) <= min(t1,t2), t1>=0, t2>=0, t3>=0];
optimize(C,obj);
Powers of posynomials are allowed in generalized geometric programs. YALMIP will automatically take care of this and convert the problems to a standard geometric programs. Note that the power has to be positive if used on the left-hand side of a <=, and negative otherwise.
sdpvar t1 t2 t3
obj = (40*t1^-1*t2^-0.5*t3^-1)+(20*t1*t3)+(40*t1*t2*t3);
C = [max((1/3)*t1^-2*t2^-2+(4/3)*t2^0.5*t3^-1,0.25*t1*t2) <= min((t1+0.5*t2)^-1,t2)];
C = [C, (2*t1+3*t2^-1)^0.5 <= 2, t1>=0, t2>=0, t3>=0];
optimize(C,obj);
To understand how a generalized geometric program can be converted to a standard geometric program, the reader is referred to [Boyd et al 2007].
The posynomial geometric programming problem is not convex in its standard formulation. The presence of multiple singularities due to the negative powers does not make matters ny easier. Hence, if a general nonlinear solver is applied to the problem, it will typically fail. However, by performing a suitable logarithmic variable transformation, the problem is rendered convex. YALMIP has built-in support for performing this variable change, and solve the problem using a nonlinear solver such as FMINCON. To invoke this module in YALMIP, use the solver tag `fmincon-geometric’.
sdpvar t1 t2 t3
obj = (40*t1^-1*t2^-0.5*t3^-1)+(20*t1*t3)+(40*t1*t2*t3);
C = [(1/3)*t1^-2*t2^-2+(4/3)*t2^0.5*t3^-1 <= 1, t1>=0, t2>=0, t3>=0];
optimize(C,obj,sdpsettings('solver','fmincon-geometric'));
The mixed-integer branch and bound solver in YALMIP is built in a modular fashion that makes it possible to solve almost arbitrary convex mixed integer programs. The following example is taken from [Boyd et al 2007]. To begin with, define the data for the example.
a = ones(7,1);
alpha = ones(7,1);
beta = ones(7,1);
gamma = ones(7,1);
f = [1 0.8 1 0.7 0.7 0.5 0.5]';
e = [1 2 1 1.5 1.5 1 2]';
Cout6 = 10;
Cout7 = 10;
Introduce symbolic expressions used in the model.
x = sdpvar(7,1);
C = alpha+beta.*x;
A = sum(a.*x);
P = sum(f.*e.*x);
R = gamma./x;
D1 = R(1)*(C(4));
D2 = R(2)*(C(4)+C(5));
D3 = R(3)*(C(5)+C(7));
D4 = R(4)*(C(6)+C(7));
D5 = R(5)*(C(7));
D6 = R(6)*Cout6;
D7 = R(7)*Cout7;
Define the objective function and constraints, and solve the problem.
% Constraints
F = [x >= 1, P <= 20, A <= 100];
% Objective
D = max([(D1+D4+D6),(D1+D4+D7),(D2+D4+D6),(D2+D4+D7),(D2+D5+D7),(D3+D5+D6),(D3+D7)]);
% Solve!
optimize([F, integer(x)],D)
value(D)
ans =
8.3333
An alternative model is discussed in the paper, and is just as easy to define.
T1 = D1;
T2 = D2;
T3 = D3;
T4 = max(T1,T2)+D4;
T5 = max(T2,T3) + D5;
T6 = T4 + D6;
T7 = max([T3 T4 T5]) + D7;
D = max(T6,T7);
optimize([F,integer(x)],D)
value(D)
Confusion can occur in the reformulation engine if you have convex quadratic constraints in your geometric program. To avoid this problem, use sdpsettings('convertconvexquad',0). To avoid some other known issues, it is advised to explicitly tell YALMIP that the problem is a geometric problem by specifying the solver to 'gpposy', 'mosek-geometric' or 'fmincon-geometric'.
Never use the commands sqrt and cpower when working with geometric programs, i.e. always use the ^ operator. The reason is implementation issues in YALMIP. The commands sqrt and cpower are meant to be used in optimization problems where a conic second-order cone model is meant to be derived.