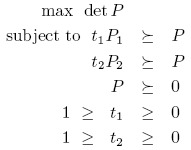
Let us solve a determinant maximization problem. Given two ellipsoids
\[\begin{align} E_1 &= \{x ~|~ x^TP_1x \leq 1\}\\ E_2 &= \{x ~|~ x^TP_2x \leq 1\}\\ \end{align}\]Find the ellipsoid \(x^TPx \leq 1\) with smallest possible volume that contains the union of \(E_1\) and \(E_2\). By using the fact that the volume of the ellipsoid is proportional to \(\det(P)\) and applying the S-procedure, it can be shown that this problem can be written as
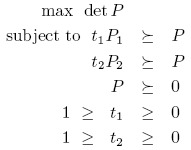
The objective function \(-\det(P)\) (which is minimized) is not convex, but monotonic transformations can render this problem convex. One alternative is the logarithmic transform, leading to minimization of\(-\log(\det(P))\) instead, which only is supported if you use SDPT3 version 4 (see below).
For other SDP solvers YALMIP uses \(-\det(P)^{1/m}\) where \(m\) is dimension of \(P\) (in other words, the geometric mean of the eigenvalues, which is a monotonic function of the determinant). The concave function \(\det(P)^{1/m}\), available by applying geomean on a Hermitian matrix in YALMIP, can be modeled using semidefinite and second order cones, hence any SDP solver can be used for solving determinant maximization problems.
n = 2;
P1 = randn(2);P1 = P1*P1'; % Generate random ellipsoid
P2 = randn(2);P2 = P2*P2'; % Generate random ellipsoid
t = sdpvar(2,1);
P = sdpvar(n,n);
F = [1 >= t >= 0];
F = [F, t(1)*P1-P >= 0];
F = [F, t(2)*P2-P >= 0];
sol = optimize(F,-geomean(P));
x = sdpvar(2,1);
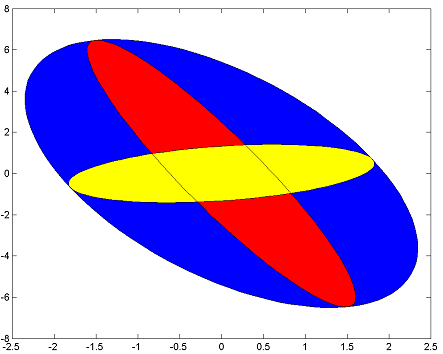
plot(x'*value(P)*x <= 1,[],'b'); hold on
plot(x'*value(P1)*x <= 1,[],'r');
plot(x'*value(P2)*x <= 1,[],'y');
If you have the dedicated solver SDPT3 installed and want to use it to handle the logarithmic term directly, you must use the dedicated command logdet for the objective and explicitly select SDPT3. This command can not be used in any other construction than in the objective function, compared to the geomean operator that can be used as any other variable in YALMIP, since it a so called nonlinear operator.
optimize(F,-logdet(P),sdpsettings('solver','sdpt3'));
x = sdpvar(2,1);
plot(x'*value(P)*x <= 1,[],'b'); hold on
plot(x'*value(P1)*x <= 1,[],'r');
plot(x'*value(P2)*x <= 1,[],'y');
Note that if you use the logdet command but not explicitly select a solver that supports logdet terms natively, YALMIP will use \(-\det(P)^{1/m}\) as objective function instead anyway. This will not cause any problems if your objective function is a simple logdet expression (since the two functions are monotonically related). However, if you have a mixed objective function such as \(\operatorname{trace}(P)-\log(\det(P))\), you can only use SDPT3 version 4.