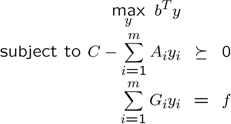
Problems in YALMIP are internally written (interpreted) in the following format (this will be referred to the dual form, or dual type representation)
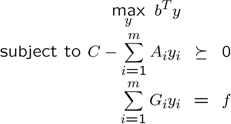
The dual to this problem is (called the primal form)
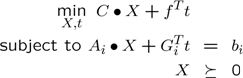
The dual (dual in the sense that it is the dual related to a user defined constraint) variable \(X\) can be obtained using YALMIP. Consider the following version of the Lyapunov stability example (of course, dual variables in LP, QP and SOCP problems can also be extracted, as long as the solver returns both a primal and a dual).
A = randn(3);A = A-eye(3)*(0.1+max(real(eig(A))));
P = sdpvar(3);
F = [P >= eye(n), A'*P+P*A <= 0];
diagnostics = optimize(F,trace(P));
The dual variables related to the constraints P>=I and A’*P+PA<=0 can be obtained by using the command dual.
Z1 = dual(F(1))
Z2 = dual(F(2))
Complementary slackness can easily be checked since value is overloaded on constraints (it returns the slack)
trace(dual(F(1))*value(F(1)))
trace(dual(F(2))*value(F(2)))
Notice, value(F(1)) returns value(0-(A’P+PA)).