Nonconvex quadratic programming and moments: 10 years later

Almost 10 years ago, a post was published, comparing semidefinite relaxation strategies with YALMIPs built-in global solvers. Although the main message of the post remains even more valid (understand when, why and how you apply a semidefinite relaxation!), the computational results are perhaps a bit outdated.

We recompute the results to reflect 3 developments over the last decade

We now have MOSEK available for solving semidefinite programs more efficiently.
The built-in global solver BMIBNB has been improved.
There are now several easily accessible external solvers for global nonconvex quadratic programming.

Hence, without further ado, we run the example again, but this time with many more solvers, and on larger problems. If you want to run this code, you will have to adjust it to the set of solvers you have available.

The code allows the solvers to use 180 seconds, and runs for increasing problem sizes until no solver manages to solve the problem in that time. We turn off display since it affects the computation time for smaller problems, but if you run the code turn it on initially to make sure things actually work (be careful with CPLEX though, it has severe bugs causing it to crash some versions of MATLAB when printing to the command window)

clear all
clf
defaults = sdpsettings('verbose',0);
maxtime = 180;
ops(1) = sdpsettings(defaults,'solver','moment','moment.order',3,'moment.solver','mosek','mosek.MSK_DPAR_OPTIMIZER_MAX_TIME',maxtime);
ops(end+1) = ops(1);ops(2).moment.order = 2;
ops(end+1) = sdpsettings(defaults,'solver','bmibnb','bmibnb.uppersolver','fmincon','bmibnb.maxtime',maxtime,'bmibnb.relgaptol',1e-4,'bmibnb.maxiter',inf);
ops(end+1) = sdpsettings(defaults,'solver','gurobi','gurobi.timelimit',maxtime);
ops(end+1) = sdpsettings(defaults,'solver','cplex','cplex.timelimit',maxtime);
ops(end+1) = sdpsettings(defaults,'solver','scip','scip.maxtime',maxtime,'scip.maxnodes',2^31-1);
ops(end+1) = sdpsettings(defaults,'solver','baron','baron.maxtime',maxtime);
ops(end+1) = sdpsettings(defaults,'solver','kktqp','kktqp.solver','gurobi','gurobi.timelimit',maxtime);

n = 1;
go_on = 1;
while go_on    
    Q = magic(n);
    x = sdpvar(n,1);
    for k = 1:length(ops)
        % Only run this solver if it finished in time for smaller model                             
        if n == 1 || comptimes(k,n-1)<maxtime
            disp(['Calling ' ops(k).solver ', n = ' num2str(n)]);
            if k == 2
                sol = optimize([-1 <= x <= 1,  x.^2 <= 1],x'*Q*x,ops(k));
            else
                sol = optimize([-1 <= x <= 1],x'*Q*x,ops(k));
            end
            comptimes(k,n) = sol.solvertime;               
        else
            comptimes(k,n) = nan;                   
        end
    end
    l=semilogy(1:n,comptimes);set(l,'linewidth',2);grid on;
    l = legend({ops.solver});
    set(l,'linewidth',2,'Location','southeast');drawnow
    n = n + 1;
    go_on = ~all(isnan(comptimes(:,end)));
end

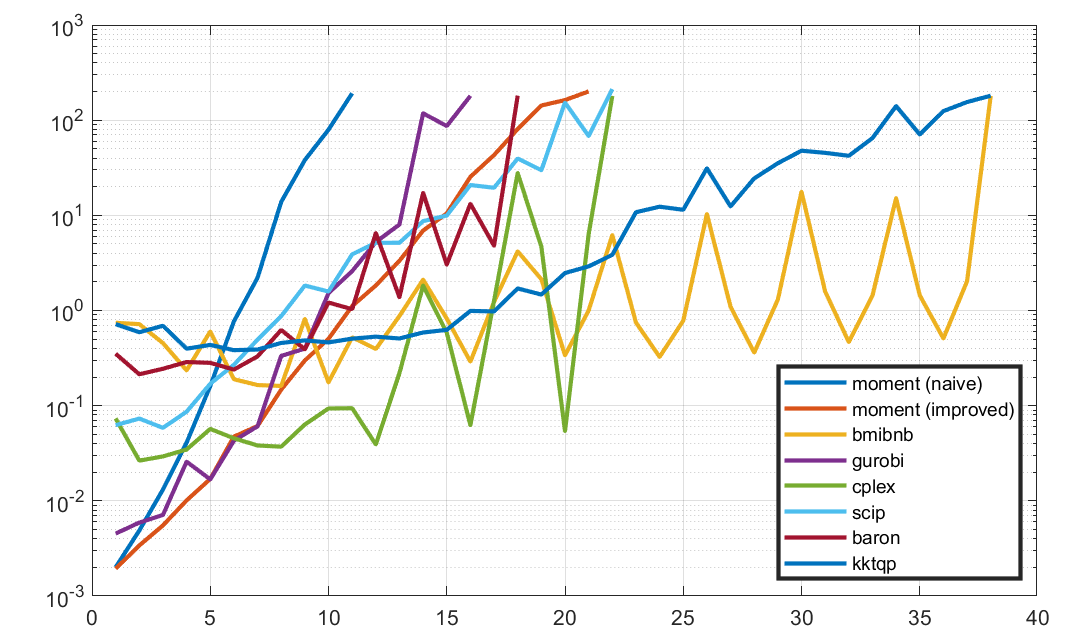
Computation results

Some general comments on what we see

Reading the figure: From left to right in giving up (crossing 180 seconds) we have full moment relaxation, Gurobi, BARON, improved moment relaxation, SCIP and Cplex, and the surprise winners BMIBNB and KKTQP
The main message remains: A full-fledged naive semidefinite relaxation is the worst you can do for anything but very small problems. A slightly improved model which is compactified using quadratic constraints allows a smaller semidefinite program that is competetive with the global solvers for a larger range of problem sizes.
A benefit with the moment based methods is that the computational effort is fairly predictable, compared to the more unpredictable behaviour of the other global solvers.
A benefit with the branch & bound based global methods is that they may find a solution very quickly and can be terminated and then also supply a lower bound. For instance, BMIBNB can almost always deliver a solution within 1% optimality gap within a few seconds (and that solution is almost always the global minimizer). In the final model with n=38, although it takes the solver more than 180 seconds to close the gap completely, the solver has found the global solution, with a gap of 0.1%, already after a fraction of a second and then spends the remaining time on trying to close the gap further. This is not possible with the moment based method. If you are lucky, it has computed a tight lower bound when it is finisihed, and from that it might be possible to extract a solution.
Results for small \(n\) are not that relevant. For these small sizes, general overhead in the MATLAB interfaces influence more than the actual algorithm. For instance, Gurobi and Mosek (used for the moment relaxation) have very low MATLAB overhead, while CPLEX is worse, and the built-in solvers KKTQP and BMIBNB are entirely coded in MATLAB which cause overhead for trivial problem sizes.
The time reported for the moment relaxations are the times spent in the SDP solver which solves the relaxation (here MOSEK). The actual call to the moment framework is larger, and becomes excessive for larger problem sizes. This is not caused by the complexity of the resulting SDP or the theory, but by the quick-n-dirty implementation of setting up the moment relaxation inside YALMIP. However, for problems of sizes where this becomes problematic, the solution time in the solver will be massive anyway so you would probably never want to solve those problems to begin with.
BMIBNB, GUROBI, CPLEX, SCIP and BARON attack the nonconvex QP using the same strategy (spatial branch & bound). The fact that BMIBNB performs extremely well here is not a general conclusion, but the result of some very effient cut or bound propagator which just happens to perform well on this model class.
Since we only allow 180 seconds, the reported times which are just above 180 seconds are most likely not solved to optimality, but the solver simply had to abort as it ran out of time.
We have made no changes to default settings. Hence most solver can most likely be adjusted to perform better, and the comparison might be unfair as they use different tolerances for checking feasibility and optimality (well we actually tightened the termination criteria for BMIBNB, it looked too good with the default setting as it almost always finished in only two nodes with the default relative gap tolerance of 0.01%, and we cranked up the maximum numbers of allowed nodes in BMIBNB and SCIP since these have very low default limits)
The problem appears to be very easy for both BMIBNB and CPLEX when \(n\) is a multiple of 4 (these models lead to a quadratic indefinite objective with many zero eigenvalues)
The fact that the two internal solvers BMIBNB and KKTP survived the game for the longest is surprising. The commercial players still have room for improvement to say the least. Once again though, this is one particular instance class (although not cherry picked, it just happened to be the one used 10 years ago) and no general conclusions can be drawn from this. All of the commercial alternatives are orders of magnitudes faster on many other problems.
The current release of all solvers have been used, except SCIP where the most recent MATLAB interface only is available for 5.0.

Johan Löfberg